2022年7月12日 星期二
复制加密 nfc卡
2022年6月29日 星期三
各種emi 探棒diy教學
Reducing EMI in buck converters
【立錡內訓課程:不藏私大公開 2.0】Buck 轉換器中的 EMI 問題與量測
https://www.richtek.com/Design%20Support/Technical%20Document/AN045
https://www.youtube.com/watch?v=agabOgQd6ZY
2022年6月1日 星期三
雅特力 針對網頁cache提出的解決方案
雅特力 針對網頁cache提出的解決方案: (2022/6/1)
你們可以在HTTP response的header加上cache-control
有加跟沒加差別就是client端第二次之後會不會從cache中抓資料
可以參考LwIP的官方範例,它的HTML source code中有包含HTTP的header, 不過沒有加上Cache-Control必須要自己添加
加上HTTP header
HTTP/1.0 200 OK
Server: lwIP/2.0.3d (http://savannah.nongnu.org/projects/lwip)
Cache-Control: max-age=31536000
Content-Length: 1751
Content-Type: text/html
length要麻煩你自己計算
BSP的代碼:
/* HTTP header */
/* "HTTP/1.0 200 OK
" (17 bytes) */
0x48,0x54,0x54,0x50,0x2f,0x31,0x2e,0x30,0x20,0x32,0x30,0x30,0x20,0x4f,0x4b,0x0d,
0x0a,
/* "Server: lwIP/2.0.3d (http://savannah.nongnu.org/projects/lwip)
" (64 bytes) */
0x53,0x65,0x72,0x76,0x65,0x72,0x3a,0x20,0x6c,0x77,0x49,0x50,0x2f,0x32,0x2e,0x30,
0x2e,0x33,0x64,0x20,0x28,0x68,0x74,0x74,0x70,0x3a,0x2f,0x2f,0x73,0x61,0x76,0x61,
0x6e,0x6e,0x61,0x68,0x2e,0x6e,0x6f,0x6e,0x67,0x6e,0x75,0x2e,0x6f,0x72,0x67,0x2f,
0x70,0x72,0x6f,0x6a,0x65,0x63,0x74,0x73,0x2f,0x6c,0x77,0x69,0x70,0x29,0x0d,0x0a,
/* "Cache-Control: max-age=31536000
" (33 bytes) */
0x43, 0x61, 0x63, 0x68, 0x65, 0x2D, 0x43, 0x6F, 0x6E, 0x74, 0x72, 0x6F, 0x6C, 0x3A,
0x20, 0x6D, 0x61, 0x78, 0x2D, 0x61, 0x67, 0x65, 0x3D, 0x33, 0x31, 0x35, 0x33, 0x36,
0x30, 0x30, 0x30, 0x0d, 0x0a,
/* "Content-Length: 1751
" (18+ bytes) */
0x43,0x6f,0x6e,0x74,0x65,0x6e,0x74,0x2d,0x4c,0x65,0x6e,0x67,0x74,0x68,0x3a,0x20,
0x31,0x37,0x35,0x31,0x0d,0x0a,
/* "Content-Type: text/html
" (27 bytes) */
0x43,0x6f,0x6e,0x74,0x65,0x6e,0x74,0x2d,0x54,0x79,0x70,0x65,0x3a,0x20,0x74,0x65,
0x78,0x74,0x2f,0x68,0x74,0x6d,0x6c,0x0d,0x0a,0x0d,0x0a,
把這段貼到你的每個HTML代碼前面試試 length改成正確的數值
範例中 ADC頁面有問題請不要測試,main page跟LED之間的切換是正常的
可以參考上圖修改每個對應的html/css/js檔
(https://drive.google.com/file/d/1bttoZ3c7rRPr_bWLez3v2o3koMQslZVr/view?usp=sharing)
2022年4月8日 星期五
2022年3月4日 星期五
单层感知器为什么不能解决异或(XOR)问题 說明及證明
參考: https://blog.csdn.net/buracag_mc/article/details/89254808
文章目录
1. 感知器模型
2. 单层感知器模型算法概述
3. 线性不可分问题
4. "与"、"或"、"非"问题的证明
5. "异或"问题的证明
5.1单层感知机不能解决"异或"问题证明方法一
5.2 单层感知机不能解决"异或"问题证明方法二
1. 感知器模型
感知器模型是美国学者罗森勃拉特(Frank Rosenblatt)为研究大脑的存储、学习和认知过程而提出的一类具有自学习能力的神经网络模型,它把神经网络的研究从纯理论探讨引向了从工程上的实现。
Rosenblatt提出的感知器模型是一个只有单层计算单元的前向神经网络,称为单层感知器。
2. 单层感知器模型算法概述
在学习基础的NN知识的时候,单个神经元的结构必定是最先提出来的,单层感知器模型算法与神经元结构类似;
大概思想是:首先把连接权和阈值初始化为较小的非零随机数,然后把有n个连接权值的输入送入网络,经加权运算处理,得到的输出如果与所期望的输出有较大的差别(对比神经元模型中的激活函数),就对连接权值参数进行自动调整,经过多次反复,直到所得到的输出与所期望的输出间的差别满足要求为止。
如下为简单起见,仅考虑只有一个输出的简单情况。设x i ( t ) x_i(t)x
i
(t)是时刻t tt感知器的输入(i=1,2,…,n),ω i ( t ) ω_i(t)ω
i
(t)是相应的连接权值,y ( t ) y(t)y(t)是实际的输出,d ( t ) d(t)d(t)是所期望的输出,且感知器的输出或者为1,或者为0。
3. 线性不可分问题
单层感知器不能表达的问题被称为线性不可分问题。 1969年,明斯基证明了“异或”问题是线性不可分问题。
4. “与”、“或”、"非"问题的证明
由于单层感知器的输出为:
y ( x 1 , x 2 ) = f ( ω 1 ∗ x 1 + ω 2 ∗ x 2 − θ ) y(x1,x2) = f(ω1 * x1 + ω2 * x2 - θ)
y(x1,x2)=f(ω1∗x1+ω2∗x2−θ)
所以,用感知器实现简单逻辑运算的情况如下:
"与"运算(And, x1∧x2)
令 ω1 = ω2 = 1,θ = 1.5,则: y = f(1 * x1 + 1 * x2 - 1.5)
显然,当x1和x2均为1时,y的值1;而当x1和x2有一个为0时,y的值就为0.
"或"运算(Or, x1∨x2)
令ω1 = ω2=1, θ = 0.5,则: y=f(1 * x1 + 1 * x2 - 0.5)
显然,只要x1和x2中有一个为1,则y的值就为1;只有当x1和x2都为0时,y的值才为0。
"非"运算(Not, ~X1)
令ω1 = -1, ω2 = O, θ = -0.5,则: y = f((-1) * x1 + 1 * x2 + 0.5)
显然,无论x2为何值,x1为1时,y的值都为0;x1为0时,y的值为1。即y总等于~x1。
"异或"运算(x1 XOR x2)
5. "异或"问题的证明
5.1单层感知机不能解决"异或"问题证明方法一
如果“异或”(XOR)问题能用单层感知器解决,则由XOR的真值映射关系如下:
(x1, x2) y
(0, 0) 0
(0, 1) 1
(1, 0) 1
(1, 1) 0
则ω1、 ω2 和θ 必须满足如下方程组:
1). ω1 + ω2 - θ < 0 --> θ > ω1 + ω2
2). ω1 + 0 - θ ≥ 0 --> 0 ≥ θ - ω1
3). 0 + 0 - θ < 0 --> θ > 0
4). 0 + ω2 - θ ≥ 0 --> 0 ≥ θ - ω2
显然,该方程组是矛盾的,无解!这就说明单层感知器是无法解决异或问题的。
5.2 单层感知机不能解决"异或"问题证明方法二
首先需要证明以下定理:
样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点集所构成的凸壳互不相交
必要性:假设样本集T线性可分,则存在一个超平面W将数据集正实例点和负实例点完全正确地划分到超平面两侧。显然两侧的点分别构成的凸壳互不相交;
充分性:假设存在两个凸壳A、B相交,且存在超平面W将A和B线性分割,令A在B的凸壳内部的点为a,因为线性可交,则A中不存在两点之间的连线与超平面W相交,而凸壳B中任意一点与A中的点的连线均与超平面W相交,则B内部的点a也与A中任一点之间的连线不与W相交,与B壳中任一点与A中的点的连线均与超平面W相交矛盾。
故:只有正负实例点所构成的两个凸壳不相交时样本集才线性可分。
显然,对于此例,负实例样本集[(0, 0), (1, 1)] 和 正实例样本集[(0, 1), (1, 0)]是二维中是不能被线性分割的
————————————————
版权声明:本文为CSDN博主「buracag_mc」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/buracag_mc/article/details/89254808
2022年3月3日 星期四
反向传播法——BackPropagation 數值驗證說明及 程式
參考: https://www.cnblogs.com/charlotte77/p/5629865.html
可以直接把数值带进去,实际的计算一下,体会一下这个过程之后再来推导公式,这样就会觉得很容易了。
说到神经网络,大家看到这个图应该不陌生:
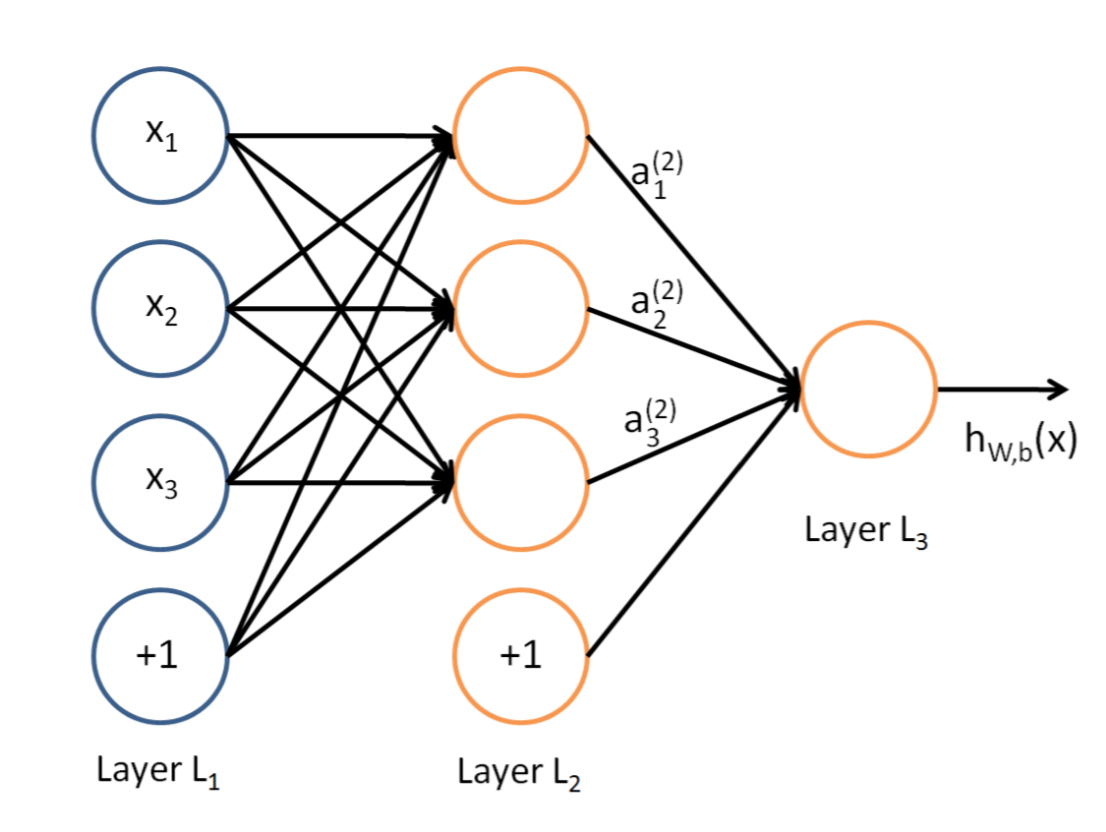
这是典型的三层神经网络的基本构成,Layer L1是输入层,Layer L2是隐含层,Layer L3是隐含层,我们现在手里有一堆数据{x1,x2,x3,...,xn},输出也是一堆数据{y1,y2,y3,...,yn},现在要他们在隐含层做某种变换,让你把数据灌进去后得到你期望的输出。如果你希望你的输出和原始输入一样,那么就是最常见的自编码模型(Auto-Encoder)。可能有人会问,为什么要输入输出都一样呢?有什么用啊?其实应用挺广的,在图像识别,文本分类等等都会用到,我会专门再写一篇Auto-Encoder的文章来说明,包括一些变种之类的。如果你的输出和原始输入不一样,那么就是很常见的人工神经网络了,相当于让原始数据通过一个映射来得到我们想要的输出数据,也就是我们今天要讲的话题。
本文直接举一个例子,带入数值演示反向传播法的过程,公式的推导等到下次写Auto-Encoder的时候再写,其实也很简单,感兴趣的同学可以自己推导下试试:)(注:本文假设你已经懂得基本的神经网络构成,如果完全不懂,可以参考Poll写的笔记:[Mechine Learning & Algorithm] 神经网络基础)
假设,你有这样一个网络层:

第一层是输入层,包含两个神经元i1,i2,和截距项b1;第二层是隐含层,包含两个神经元h1,h2和截距项b2,第三层是输出o1,o2,每条线上标的wi是层与层之间连接的权重,激活函数我们默认为sigmoid函数。
现在对他们赋上初值,如下图:
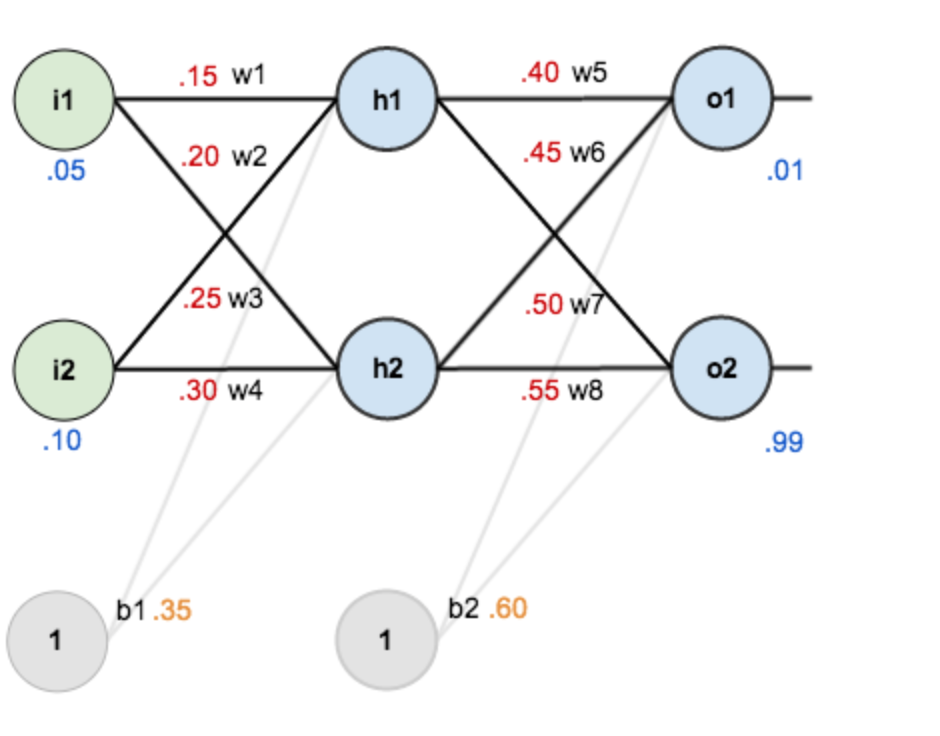
其中,输入数据 i1=0.05,i2=0.10;
输出数据 o1=0.01,o2=0.99;
初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;
w5=0.40,w6=0.45,w7=0.50,w8=0.55
目标:给出输入数据i1,i2(0.05和0.10),使输出尽可能与原始输出o1,o2(0.01和0.99)接近。
Step 1 前向传播
1.输入层---->隐含层:
计算神经元h1的输入加权和:

神经元h1的输出o1:(此处用到激活函数为sigmoid函数):
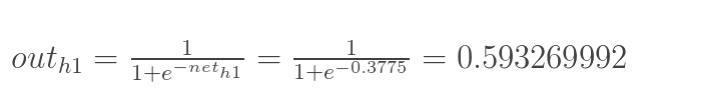
同理,可计算出神经元h2的输出o2:
![]()
2.隐含层---->输出层:
计算输出层神经元o1和o2的值:

![]()
这样前向传播的过程就结束了,我们得到输出值为[0.75136079 , 0.772928465],与实际值[0.01 , 0.99]相差还很远,现在我们对误差进行反向传播,更新权值,重新计算输出。
Step 2 反向传播
1.计算总误差
总误差:(square error)
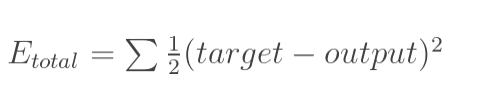
但是有两个输出,所以分别计算o1和o2的误差,总误差为两者之和:


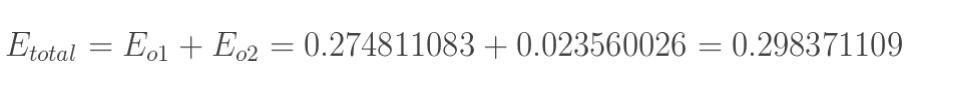
2.隐含层---->输出层的权值更新:
以权重参数w5为例,如果我们想知道w5对整体误差产生了多少影响,可以用整体误差对w5求偏导求出:(链式法则)

下面的图可以更直观的看清楚误差是怎样反向传播的:

现在我们来分别计算每个式子的值:
计算![]() :
:

计算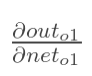 :
:

(这一步实际上就是对sigmoid函数求导,比较简单,可以自己推导一下)
计算 :
:
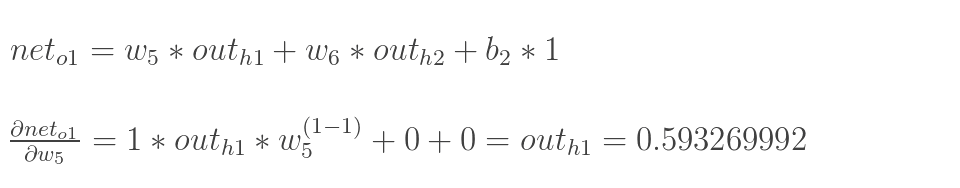
最后三者相乘:

这样我们就计算出整体误差E(total)对w5的偏导值。
回过头来再看看上面的公式,我们发现:

为了表达方便,用![]() 来表示输出层的误差:
来表示输出层的误差:

因此,整体误差E(total)对w5的偏导公式可以写成:

如果输出层误差计为负的话,也可以写成:

最后我们来更新w5的值:
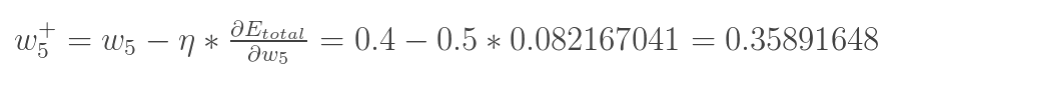
(其中,![]() 是学习速率,这里我们取0.5)
是学习速率,这里我们取0.5)
同理,可更新w6,w7,w8:

3.隐含层---->隐含层的权值更新:
方法其实与上面说的差不多,但是有个地方需要变一下,在上文计算总误差对w5的偏导时,是从out(o1)---->net(o1)---->w5,但是在隐含层之间的权值更新时,是out(h1)---->net(h1)---->w1,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差,所以这个地方两个都要计算。
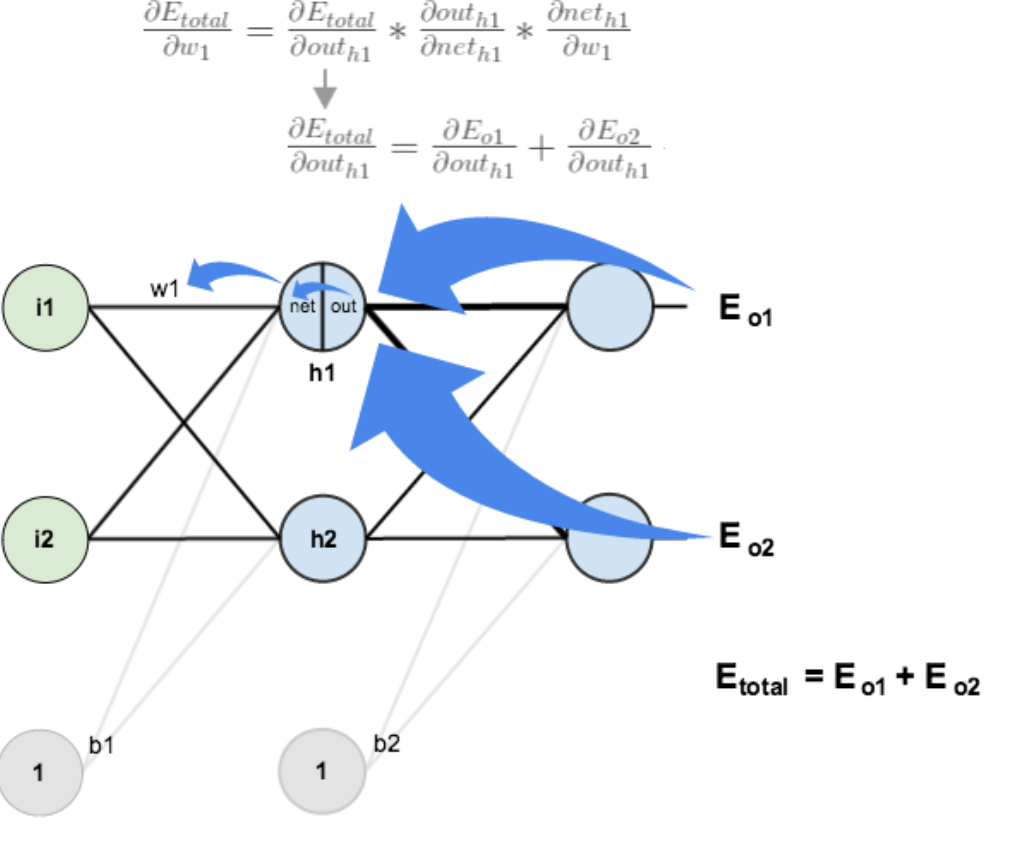
计算![]() :
:

先计算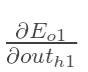 :
:
![]()
![]()
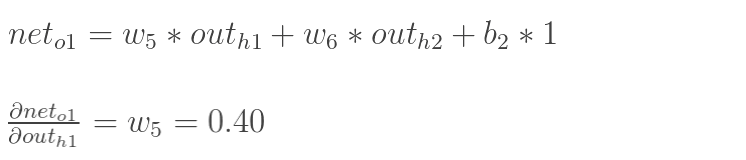
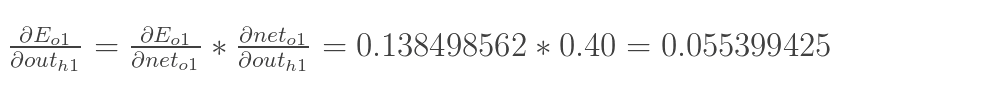
同理,计算出:
![]()
两者相加得到总值:
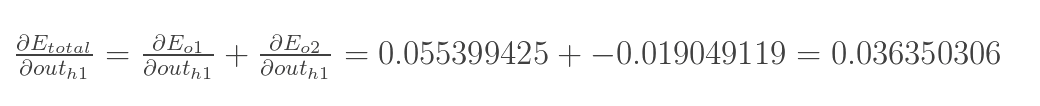
再计算![]() :
:

再计算![]() :
:

最后,三者相乘:

为了简化公式,用sigma(h1)表示隐含层单元h1的误差:

最后,更新w1的权值:
![]()
同理,额可更新w2,w3,w4的权值:

这样误差反向传播法就完成了,最后我们再把更新的权值重新计算,不停地迭代,在这个例子中第一次迭代之后,总误差E(total)由0.298371109下降至0.291027924。迭代10000次后,总误差为0.000035085,输出为[0.015912196,0.984065734](原输入为[0.01,0.99]),证明效果还是不错的。
代码(Python):
1 #coding:utf-8 2 import random 3 import math 4 5 # 6 # 参数解释: 7 # "pd_" :偏导的前缀 8 # "d_" :导数的前缀 9 # "w_ho" :隐含层到输出层的权重系数索引 10 # "w_ih" :输入层到隐含层的权重系数的索引 11 12 class NeuralNetwork: 13 LEARNING_RATE = 0.5 14 15 def __init__(self, num_inputs, num_hidden, num_outputs, hidden_layer_weights = None, hidden_layer_bias = None, output_layer_weights = None, output_layer_bias = None): 16 self.num_inputs = num_inputs 17 18 self.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias) 19 self.output_layer = NeuronLayer(num_outputs, output_layer_bias) 20 21 self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights) 22 self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights) 23 24 def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights): 25 weight_num = 0 26 for h in range(len(self.hidden_layer.neurons)): 27 for i in range(self.num_inputs): 28 if not hidden_layer_weights: 29 self.hidden_layer.neurons[h].weights.append(random.random()) 30 else: 31 self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num]) 32 weight_num += 1 33 34 def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights): 35 weight_num = 0 36 for o in range(len(self.output_layer.neurons)): 37 for h in range(len(self.hidden_layer.neurons)): 38 if not output_layer_weights: 39 self.output_layer.neurons[o].weights.append(random.random()) 40 else: 41 self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num]) 42 weight_num += 1 43 44 def inspect(self): 45 print('------') 46 print('* Inputs: {}'.format(self.num_inputs)) 47 print('------') 48 print('Hidden Layer') 49 self.hidden_layer.inspect() 50 print('------') 51 print('* Output Layer') 52 self.output_layer.inspect() 53 print('------') 54 55 def feed_forward(self, inputs): 56 hidden_layer_outputs = self.hidden_layer.feed_forward(inputs) 57 return self.output_layer.feed_forward(hidden_layer_outputs) 58 59 def train(self, training_inputs, training_outputs): 60 self.feed_forward(training_inputs) 61 62 # 1. 输出神经元的值 63 pd_errors_wrt_output_neuron_total_net_input = [0] * len(self.output_layer.neurons) 64 for o in range(len(self.output_layer.neurons)): 65 66 # ∂E/∂zⱼ 67 pd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(training_outputs[o]) 68 69 # 2. 隐含层神经元的值 70 pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons) 71 for h in range(len(self.hidden_layer.neurons)): 72 73 # dE/dyⱼ = Σ ∂E/∂zⱼ * ∂z/∂yⱼ = Σ ∂E/∂zⱼ * wᵢⱼ 74 d_error_wrt_hidden_neuron_output = 0 75 for o in range(len(self.output_layer.neurons)): 76 d_error_wrt_hidden_neuron_output += pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].weights[h] 77 78 # ∂E/∂zⱼ = dE/dyⱼ * ∂zⱼ/∂ 79 pd_errors_wrt_hidden_neuron_total_net_input[h] = d_error_wrt_hidden_neuron_output * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_input() 80 81 # 3. 更新输出层权重系数 82 for o in range(len(self.output_layer.neurons)): 83 for w_ho in range(len(self.output_layer.neurons[o].weights)): 84 85 # ∂Eⱼ/∂wᵢⱼ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢⱼ 86 pd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho) 87 88 # Δw = α * ∂Eⱼ/∂wᵢ 89 self.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight 90 91 # 4. 更新隐含层的权重系数 92 for h in range(len(self.hidden_layer.neurons)): 93 for w_ih in range(len(self.hidden_layer.neurons[h].weights)): 94 95 # ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢ 96 pd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_weight(w_ih) 97 98 # Δw = α * ∂Eⱼ/∂wᵢ 99 self.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weight 100 101 def calculate_total_error(self, training_sets): 102 total_error = 0 103 for t in range(len(training_sets)): 104 training_inputs, training_outputs = training_sets[t] 105 self.feed_forward(training_inputs) 106 for o in range(len(training_outputs)): 107 total_error += self.output_layer.neurons[o].calculate_error(training_outputs[o]) 108 return total_error 109 110 class NeuronLayer: 111 def __init__(self, num_neurons, bias): 112 113 # 同一层的神经元共享一个截距项b 114 self.bias = bias if bias else random.random() 115 116 self.neurons = [] 117 for i in range(num_neurons): 118 self.neurons.append(Neuron(self.bias)) 119 120 def inspect(self): 121 print('Neurons:', len(self.neurons)) 122 for n in range(len(self.neurons)): 123 print(' Neuron', n) 124 for w in range(len(self.neurons[n].weights)): 125 print(' Weight:', self.neurons[n].weights[w]) 126 print(' Bias:', self.bias) 127 128 def feed_forward(self, inputs): 129 outputs = [] 130 for neuron in self.neurons: 131 outputs.append(neuron.calculate_output(inputs)) 132 return outputs 133 134 def get_outputs(self): 135 outputs = [] 136 for neuron in self.neurons: 137 outputs.append(neuron.output) 138 return outputs 139 140 class Neuron: 141 def __init__(self, bias): 142 self.bias = bias 143 self.weights = [] 144 145 def calculate_output(self, inputs): 146 self.inputs = inputs 147 self.output = self.squash(self.calculate_total_net_input()) 148 return self.output 149 150 def calculate_total_net_input(self): 151 total = 0 152 for i in range(len(self.inputs)): 153 total += self.inputs[i] * self.weights[i] 154 return total + self.bias 155 156 # 激活函数sigmoid 157 def squash(self, total_net_input): 158 return 1 / (1 + math.exp(-total_net_input)) 159 160 161 def calculate_pd_error_wrt_total_net_input(self, target_output): 162 return self.calculate_pd_error_wrt_output(target_output) * self.calculate_pd_total_net_input_wrt_input(); 163 164 # 每一个神经元的误差是由平方差公式计算的 165 def calculate_error(self, target_output): 166 return 0.5 * (target_output - self.output) ** 2 167 168 169 def calculate_pd_error_wrt_output(self, target_output): 170 return -(target_output - self.output) 171 172 173 def calculate_pd_total_net_input_wrt_input(self): 174 return self.output * (1 - self.output) 175 176 177 def calculate_pd_total_net_input_wrt_weight(self, index): 178 return self.inputs[index] 179 180 181 # 文中的例子: 182 183 nn = NeuralNetwork(2, 2, 2, hidden_layer_weights=[0.15, 0.2, 0.25, 0.3], hidden_layer_bias=0.35, output_layer_weights=[0.4, 0.45, 0.5, 0.55], output_layer_bias=0.6) 184 for i in range(10000): 185 nn.train([0.05, 0.1], [0.01, 0.09]) 186 print(i, round(nn.calculate_total_error([[[0.05, 0.1], [0.01, 0.09]]]), 9)) 187 188 189 #另外一个例子,可以把上面的例子注释掉再运行一下: 190 191 # training_sets = [ 192 # [[0, 0], [0]], 193 # [[0, 1], [1]], 194 # [[1, 0], [1]], 195 # [[1, 1], [0]] 196 # ] 197 198 # nn = NeuralNetwork(len(training_sets[0][0]), 5, len(training_sets[0][1])) 199 # for i in range(10000): 200 # training_inputs, training_outputs = random.choice(training_sets) 201 # nn.train(training_inputs, training_outputs) 202 # print(i, nn.calculate_total_error(training_sets))
最后写到这里就结束了,现在还不会用latex编辑数学公式,本来都直接想写在草稿纸上然后扫描了传上来,但是觉得太影响阅读体验了。以后会用公式编辑器后再重把公式重新编辑一遍。稳重使用的是sigmoid激活函数,实际还有几种不同的激活函数可以选择,具体的可以参考文献[3],最后推荐一个在线演示神经网络变化的网址:http://www.emergentmind.com/neural-network,可以自己填输入输出,然后观看每一次迭代权值的变化,很好玩~如果有错误的或者不懂的欢迎留言:)
参考文献:
1.Poll的笔记:[Mechine Learning & Algorithm] 神经网络基础(http://www.cnblogs.com/maybe2030/p/5597716.html#3457159 )
2.Rachel_Zhang:http://blog.csdn.net/abcjennifer/article/details/7758797
3.http://www.cedar.buffalo.edu/%7Esrihari/CSE574/Chap5/Chap5.3-BackProp.pdf
4.https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/
我改過的程式 修正他程式中的問題(calculate_total_error多跑self.feed_forward)
#!/usr/bin/env python
# coding: utf-8
# In[1]:
原始網站
https://github.com/mattm/simple-neural-network
#從數值解釋 反向传播
#一文弄懂神经网络中的反向传播法——BackPropagation
#https://www.cnblogs.com/charlotte77/p/5629865.html
# In[2]:
import random
import math
import time
#
# 参数解释:
# "pd_" :偏导的前缀
# "d_" :导数的前缀
# "w_ho" :隐含层到输出层的权重系数索引
# "w_ih" :输入层到隐含层的权重系数的索引
# In[3]:
class NeuralNetwork:
#LEARNING_RATE = 0.5
hidden_layer_outputs=0
layer_outputs=0
pd_errors_wrt_output_neuron_total_net_input=0
def __init__(self, num_inputs, num_hidden, num_outputs, hidden_layer_weights = None, hidden_layer_bias = None, output_layer_weights = None, output_layer_bias = None,learing_rate=0.5):
self.num_inputs = num_inputs
self.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias)
self.output_layer = NeuronLayer(num_outputs, output_layer_bias)
self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights)
self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights)
self.LEARNING_RATE=learing_rate
def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights):
weight_num = 0
for h in range(len(self.hidden_layer.neurons)):
for i in range(self.num_inputs):
if not hidden_layer_weights:
self.hidden_layer.neurons[h].weights.append(random.random())
else:
self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num])
weight_num += 1
def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights):
weight_num = 0
for o in range(len(self.output_layer.neurons)):
for h in range(len(self.hidden_layer.neurons)):
if not output_layer_weights:
self.output_layer.neurons[o].weights.append(random.random())
else:
self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num])
weight_num += 1
def inspect(self):
print('------')
print('* Inputs: {}'.format(self.num_inputs))
print('------')
print('Hidden Layer')
self.hidden_layer.inspect()
print('------')
print('* Output Layer')
self.output_layer.inspect()
print('------')
def feed_forward(self, inputs):
self.hidden_layer_outputs=self.hidden_layer.feed_forward(inputs)
self.layer_outputs=self.output_layer.feed_forward(self.hidden_layer_outputs)
if Debug_function==1 :
print('输入层---->隐含层: 神经元H的输出 ',nn.hidden_layer_outputs)
print('隐含层---->输出层: 输出层O神经元',nn.layer_outputs)
return self.layer_outputs
def train(self, training_inputs, training_outputs):
self.feed_forward(training_inputs) #前向传播
# 1. 输出神经元的值
pd_errors_wrt_output_neuron_total_net_input = [0] * len(self.output_layer.neurons)
for o in range(len(self.output_layer.neurons)):
# ∂E/∂zⱼ
pd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(training_outputs[o])
if Debug_function==1 :
print('整体误差E(total)对netO的偏导值',pd_errors_wrt_output_neuron_total_net_input[o])
self.pd_errors_wrt_output_neuron_total_net_input=pd_errors_wrt_output_neuron_total_net_input
# 2. 隐含层神经元的值
pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons)
for h in range(len(self.hidden_layer.neurons)):
# dE/dyⱼ = Σ ∂E/∂zⱼ * ∂z/∂yⱼ = Σ ∂E/∂zⱼ * wᵢⱼ
d_error_wrt_hidden_neuron_output = 0
for o in range(len(self.output_layer.neurons)):
d_error_wrt_hidden_neuron_output += pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].weights[h]
# ∂E/∂zⱼ = dE/dyⱼ * ∂zⱼ/∂
pd_errors_wrt_hidden_neuron_total_net_input[h] = d_error_wrt_hidden_neuron_output * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_input()
# 3. 更新输出层权重系数
for o in range(len(self.output_layer.neurons)):
for w_ho in range(len(self.output_layer.neurons[o].weights)):
# ∂Eⱼ/∂wᵢⱼ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢⱼ
pd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho)
# Δw = α * ∂Eⱼ/∂wᵢ
self.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight
if Debug_function==1 :
print('更新權重o ',self.output_layer.neurons[o].weights[w_ho])
#output_layer_weights=self.output_layer.neurons
# 4. 更新隐含层的权重系数
for h in range(len(self.hidden_layer.neurons)):
for w_ih in range(len(self.hidden_layer.neurons[h].weights)):
# ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢ
pd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_weight(w_ih)
# Δw = α * ∂Eⱼ/∂wᵢ
self.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weight
if Debug_function==1 :
print('更新權重h ',self.hidden_layer.neurons[h].weights[w_ih])
def calculate_total_error(self, training_sets): #总误差
total_error = 0
for t in range(len(training_sets)):
# #when training_sets=[[[0.05, 0.1], [0.01, 0.99]]] then training_inputs=[0.05, 0.1] training_outputs=[0.01, 0.99]
training_inputs, training_outputs = training_sets[t]
#self.feed_forward(training_inputs) #原始範例有誤 加上此行會有異常輸出
for o in range(len(training_outputs)): #len(training_outputs)=2
#print('len(training_outputs)',len(training_outputs))
#print(training_outputs)
single_error=self.output_layer.neurons[o].calculate_error(training_outputs[o]) #有两个输出,所以分别计算o1和o2的误差,总误差为两者之和
if Debug_function==1 :
print('输出o的误差',single_error)
total_error += single_error
return total_error
# In[4]:
class NeuronLayer:
def __init__(self, num_neurons, bias):
# 同一层的神经元共享一个截距项b
self.bias = bias if bias else random.random()
self.neurons = []
for i in range(num_neurons):
self.neurons.append(Neuron(self.bias))
def inspect(self):
print('Neurons:', len(self.neurons))
for n in range(len(self.neurons)):
print(' Neuron', n)
for w in range(len(self.neurons[n].weights)):
print(' Weight:', self.neurons[n].weights[w])
print(' Bias:', self.bias)
def feed_forward(self, inputs):
outputs = []
for neuron in self.neurons:
outputs.append(neuron.calculate_output(inputs))
return outputs
def get_outputs(self):
outputs = []
for neuron in self.neurons:
outputs.append(neuron.output)
return outputs
# In[5]:
class Neuron:
def __init__(self, bias):
self.bias = bias
self.weights = []
def calculate_output(self, inputs):
self.inputs = inputs
calculate_total_net_input=self.calculate_total_net_input()
if Debug_function==1 :
print('计算神经元的输入加权和',calculate_total_net_input)
self.output = self.squash(calculate_total_net_input)
return self.output
def calculate_total_net_input(self):
total = 0
for i in range(len(self.inputs)):
total += self.inputs[i] * self.weights[i]
return total + self.bias
# 激活函数sigmoid
def squash(self, total_net_input):
return 1 / (1 + math.exp(-total_net_input))
def calculate_pd_error_wrt_total_net_input(self, target_output):
derivative_Etotal_out=self.calculate_pd_error_wrt_output(target_output)
derivative_Etotal_net=self.calculate_pd_total_net_input_wrt_input()
if Debug_function==1 :
print('偏微分total/out=',derivative_Etotal_out)
print('偏微分total/net=',derivative_Etotal_net)
return derivative_Etotal_out * derivative_Etotal_net;
# 每一个神经元的误差是由平方差公式计算的
def calculate_error(self, target_output):
return 0.5 * (target_output - self.output) ** 2
def calculate_pd_error_wrt_output(self, target_output):
return -(target_output - self.output)
def calculate_pd_total_net_input_wrt_input(self):
return self.output * (1 - self.output)
def calculate_pd_total_net_input_wrt_weight(self, index):
return self.inputs[index]
# In[36]:
#主函數
#目标:给出输入数据i1,i2(0.05和0.10),使输出尽可能与原始输出o1,o2(0.01和0.99)接近。自動調整 權重等參數
Debug_function=0; #全域變數 Debug_function=1 顯示相關細節
input_data=[0.05, 0.1] #輸入的數據
output_data=[0.01, 0.99] #輸出的數據
hidden_layer_number=2 #隱藏層的數量
hidden_layer_bias=0.35 #隱藏層的基數
output_layer_bias=0.6 #輸出層的基數
learing_rate=0.5 #學習率
def final():
#Step 1 前向传播
print('輸入層---->隱含層: 神經元H的輸出 ',nn.hidden_layer_outputs)
print('隱含層---->輸出層: 輸出層O神經元',nn.layer_outputs)
#Step 2 反向传播
print('總誤差=',round(nn.calculate_total_error([[input_data,output_data]]), 9))
print('整體誤差E(total)對netO的偏導值',nn.pd_errors_wrt_output_neuron_total_net_input)
print(' ')
''' #參數說明
NeuralNetwork參數: num_inputs, num_hidden, num_outputs, hidden_layer_weights = None, \
hidden_layer_bias = None, output_layer_weights = None, output_layer_bias = None,learing_rate
'''
''' #原始範例
nn = NeuralNetwork(2, 2, 2, hidden_layer_weights=[0.15, 0.2, 0.25, 0.3], hidden_layer_bias=0.35,\
output_layer_weights=[0.4, 0.45, 0.5, 0.55], output_layer_bias=0.6,learing_rate=0.5)
'''
start_time = time.time()
#以下 hidden_layer_weights及output_layer_weightsg使用亂數
nn = NeuralNetwork(num_inputs=len(input_data), num_hidden=hidden_layer_number, num_outputs=len(output_data),hidden_layer_bias=hidden_layer_bias, output_layer_bias=output_layer_bias,learing_rate=learing_rate)
'''
#以下自訂 hidden_layer_weights及output_layer_weightsg使用指定數值 但請注意weights欄位需與輸入的資料內容數量匹配
nn = NeuralNetwork(num_inputs=len(input_data), num_hidden=hidden_layer_number,\
num_outputs=len(output_data),hidden_layer_bias=hidden_layer_bias,\
output_layer_bias=output_layer_bias,learing_rate=learing_rate,\
hidden_layer_weights=[0.15, 0.2, 0.25, 0.3],output_layer_weights=[0.4, 0.45, 0.5, 0.55])
'''
for i in range(10000):
#train參數: training_inputs, training_outputs
#nn.train([0.05, 0.1], [0.01, 0.99])
nn.train(input_data,output_data)
#print('第',i,'次train')
#final()
end_time = time.time()
elapsed_time = end_time - start_time
print('計算花的時間 {} seconds'.format(elapsed_time))
print('最終計算結果:')
final()
print('權重:')
for o in range(len(nn.output_layer.neurons)):
for w_ho in range(len(nn.output_layer.neurons[o].weights)):
print('h',o,'o',w_ho,'=',nn.output_layer.neurons[o].weights[w_ho])
for h in range(len(nn.hidden_layer.neurons)):
for w_ih in range(len(nn.hidden_layer.neurons[h].weights)):
print('i',h,'h',w_ih,'=',nn.hidden_layer.neurons[h].weights[w_ih])
# In[7]:
#另外一个例子,可以把上面的例子注释掉再运行一下:
training_sets = [
[[0, 0], [0]],
[[0, 1], [1]],
[[1, 0], [1]],
[[1, 1], [0]]
]
nn = NeuralNetwork(len(training_sets[0][0]), 5, len(training_sets[0][1]))
for i in range(10000):
training_inputs, training_outputs = random.choice(training_sets)
nn.train(training_inputs, training_outputs)
print(i, '总误差',nn.calculate_total_error(training_sets))
